【完全解説】平均値・中央値・最頻値を図を用いて説明します

それぞれの違いを説明できますか？

数学や統計でよく出てくる3つのワードがあります

この違いを説明できますか？

そして違いを意識して活用できていますか？

今回はこの3つの違いをご説明します

分かりにくい理由

この3つの統計ワードが、非常に理解しにくいことには原因があります

それは単純で…日常で使わないからです

ニュースなどで「平均」という言葉はよく耳にしますが、

中央値・最頻値はほぼ出会うことはありません

しかし、データ分析を実施すると、意外と利用頻度が高くなります

そこで今回は「学校のテスト」という皆さんが理解しやすいテーマで説明を進めていきます

サンプル：テストの点数

事例として学校のテストの点数を使い、平均値・中央値・最頻値を説明します

クラスは全員で20人とします

3つの代表値の説明

平均値・中央値・最頻値を説明するには棒グラフ（ヒストグラム）が分かりやすいため、

都度グラフを用いて説明します

また他サイトの説明と違い、計算式は使いません

平均値

平均値の説明は、「点数を合計したものを人数で割る」となります

想像しやすいのはこのようなグラフではないでしょうか？

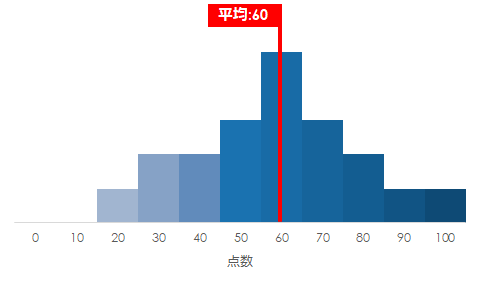
もちろんこの認識は間違いではありません

ほとんどの平均値は図のような正規分布（山なりなグラフ）になります

しかし平均には落とし穴があります

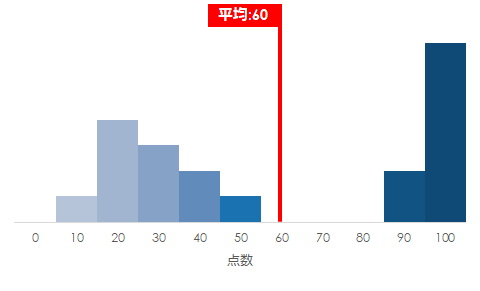
こちらのグラフは別のテストの結果です

高い点を取った人と低い点を取った人に大きく二分されています

平均点は最初のグラフと同じ60点となりますが、実際に60点を取った人はいません

つまり平均は大きく偏ったデータに不向きと言えます

この偏りを考慮に入れるために中央値・最頻値を活用します

中央値

中央値とは人数のちょうど半分の人の点数のことです

偶数の場合は中央の2人を平均した結果になります

つまり20人のクラスでは、高得点順に並んで10人目と11人目の平均が中央値になります

下記のグラフは山なりの点数プロットのため、平均値と中央値が同じになります

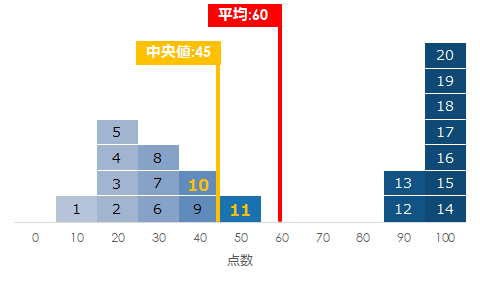
一方でデータに偏りがある場合は、平均値と中央値が異なります

この場合は平均値=60より中央値=45の方が小さくなります

※四分位数

中央値を学んだついでに四分位数をご説明します

四分位数とはデータを4つに均等配分した数値です

中央値で前半と後半に分けたときの、中央値という考え方もできます

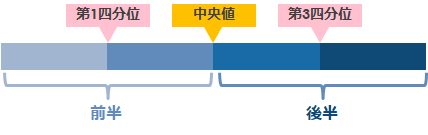
4つに分けたうち1と2の間が「第1四分位数」で3と4の間が「第3四分位数」と呼びます

先ほどのグラフに四分位数を入れると、下記のようになります

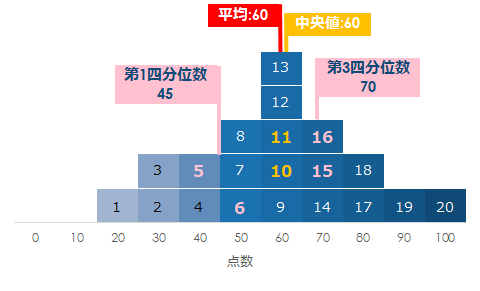
そして偏ったデータの場合も同様に四分位数を追加します

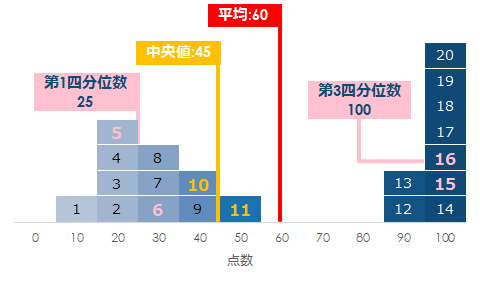
最頻値

最頻値はその名の通り、最も頻度が高い値（点数）のことです

グラフにすると一番人数が多くなる山頂の部分です

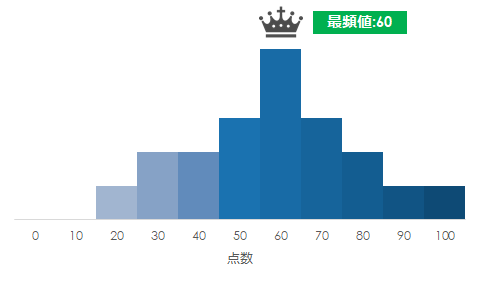
もちろん最頻値が100点の場合もあります

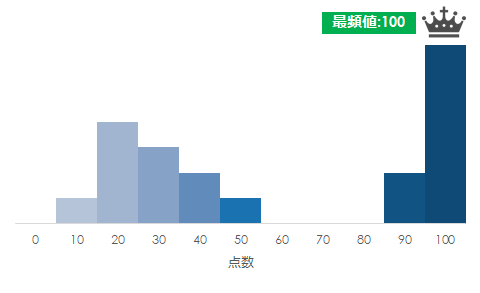
まとめ

今回は3+1つの代表値についてご紹介してきました

理解しにくい場合はグラフ（ヒストグラム）を頭に浮かべて考えてみてください