目次
ポケモンデータを使って代表値を学ぶ
ポケモンのデータを使ってデータ分析を学ぶ企画の第二弾です
今回はデータをざっくり把握するための代表値をご紹介します
そしてテーマとして下記を設定し、ポケモンのデータ分析を実施します
ステータスが全ポケモンの「真ん中」にいる1匹を見つけ出す
ポケモンデータの中身に関しては、第一弾の記事をご覧ください
 ポケモンで学ぶデータ分析|データの中身を知ろう
ポケモンで学ぶデータ分析|データの中身を知ろう 代表値とは?
今回ご紹介する代表値とは、データの大枠を知ることができる指標です
代表値の確認は、データ分析の初手で実施する手法です
データ(ポケモン)を一つずつ見ていくのは非常に大変ですし、時間がかかってしまいます
そこでデータがどういう形をしているかを、代表値という形見ていきましょう
代表値(平均値・中央値・最頻値)についてはこちらの記事をご覧ください
 【完全解説】平均値・中央値・最頻値を図を用いて説明します
【完全解説】平均値・中央値・最頻値を図を用いて説明します 全ポケモンの代表値を見てみる
代表値を見るために、全てのポケモンのステータスを見ていきます
※ちなみに一番ステータスが高いのは「アルセウス」というポケモンです

単純に代表値を見るだけでは、データを集計して終わりになってしまいます
それだけでは「データ分析」をしたとは言えません
最終的に「示唆」を出すこと、そして「アクション」を起こすことがデータ分析の基本です
そこで一つのテーマを設けてデータ分析を進めていきます
ステータスが全ポケモンの「真ん中」にいる1匹を見つけ出す
「真ん中」をどういう定義にするかが難しいので、代表値をそれぞれ見ていきましょう
平均値
平均値とは「全ポケモンのステータスを合計し、ポケモン数で割る」ことで算出が可能です
平均値を算出すると「423」という結果が出てきました
このままだと分かりにくいので、「フシギダネ」の進化系列と比較してみましょう
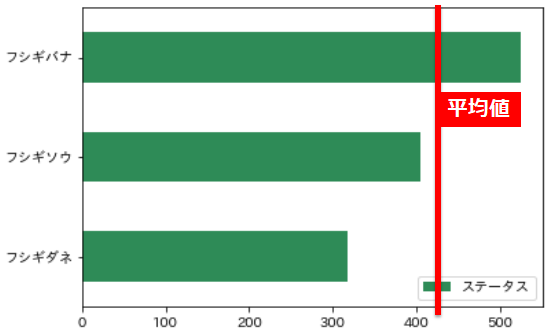
3匹の平均ではなく、全ポケモンの平均値をプロットしています
「フシギソウ」より少しだけ強く、フシギバナよりも弱いというのが
全ポケモンのステータスの平均値をとった場合の示唆でした
それではこの平均値に一番近いポケモンを探してみましょう
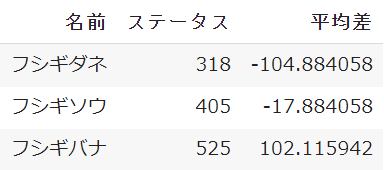
まずはすべてのポケモンのステータスから平均値(423)を引きます
例えば「フシギダネ」のステータスは318なので、引き算をすると-105の差が出ました
全てのポケモンをグラフにプロットしてみます
下記グラフは中心にいるほど、平均との差が無い=中心に近いということになります
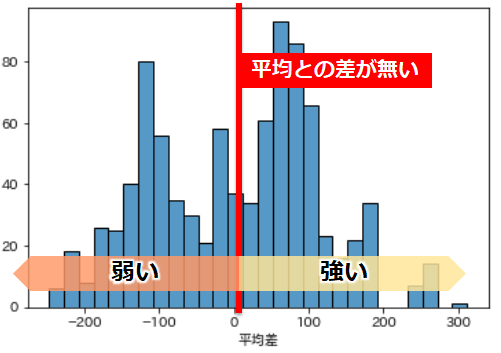
最後に平均との差が「0」に一番近いポケモンを見つけてみましょう
調べてみると差分が「0.12」しかないポケモンがいました…
それは「ホルード」というポケモン(筆者は知らないポケモンでした…)

中央値
続いて中央値を見ていきます
中央値はポケモンをステータス順に並べて、真ん中の値を指します
平均値はとびぬけたステータスを持ったポケモンがいると偏ってしまうのに対し、中央値はとびぬけた値(外れ値)に左右されません
定義に沿って全ポケモンのステータスの中央値を取ると「440」という数値が出てきました
先ほどの「フシギダネ」の進化系列に中央値も追加してみます
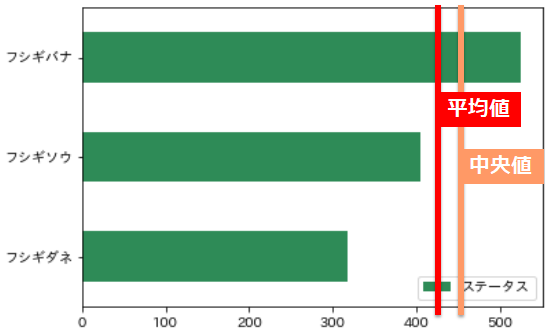
平均値より若干高くなりました
そして平均との差と同様に、中央値の差分を算出し、差が小さいポケモンを見つけます
なんと中央値「440」に該当するポケモンは10匹ほどいました
その中の一匹が「ペルシアン」というポケモンでした

最頻値
最後に最頻値をご紹介します
最頻値とは文字通り「最も多く登場する値」です
(正規分布の)データは平均値が最頻値になることが多いです
さてポケモンのステータスではどうでしょうか?
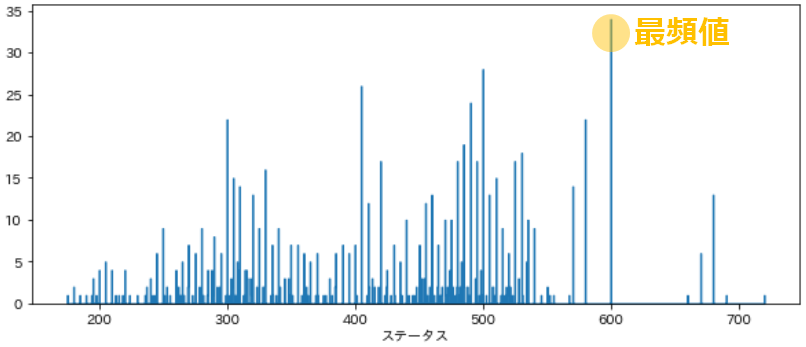
予想に反してポケモンのステータスの最頻値は「600」となりました
グラフを見ると200~500あたりは分散してしまっているのが分かります
ポケモンには600族と呼ばれる、最終進化の合計種族値が600になるポケモンがいる

伝説のポケモン含めて強そうなポケモンが並んでいます
これはテーマである全ポケモンのステータスの真ん中に反すると判断し、考慮に入れないことにしました
分析結果はいかに!?
最後に代表値を利用し、テーマに当てはまるポケモンを見つけ出したいと思います
改めてテーマはこちら↓
ステータスが全ポケモンの「真ん中」にいる1匹を見つけ出す
「平均値」と「中央値」のどちらを利用するか最後まで迷ったので
どちらも考慮に入れることにしました
平均値と中央値の差分を合計したものが、0に近い(差が無い)ポケモンを集計します
最終的に算出した結果がこちら
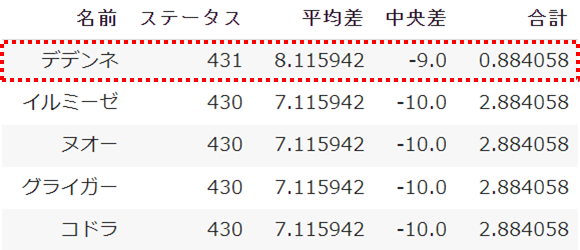
平均値と中央値の差分で一番近いのは「デデンネ」というポケモンでした
なんともかわいいポケモンで、ピカチュウと似ている気も…

まとめ
今回はポケモンのデータを使ってデータ分析を学ぶ企画の第二弾でした
そして改めてテーマはこちら
ステータスが全ポケモンの「真ん中」にいる1匹を見つけ出す
そして平均値と中央値、最頻値を使いだした結果は、「デデンネ」というポケモンでした
次の記事では知っているようで知らない「相関関係」についてご紹介します
 相関関係とは?分かりやすく解説|ポケモンで学ぶデータ分析
相関関係とは?分かりやすく解説|ポケモンで学ぶデータ分析 
 Smart-Hint
Smart-Hint 

