Smart-Hint 
目次
回帰分析をポケモンのデータで学ぶ
今回は回帰分析（かいきぶんせき）という、非常に便利な分析手法についてご紹介していきます
「単回帰分析」や「重回帰分析」とも呼ばれており、データを利用して未知のものに対する「予測」を実施する手法です
様々な手法がある回帰分析ですが、最も基本的な「線形回帰」についてご説明していきます
この分析手法について実際のデータをもとに分析を進めるため、誰にでも馴染みのあるポケモンのデータで解説していきます
回帰分析とは？
回帰分析
連続尺度の従属変数（目的変数）Y と独立変数（説明変数）X の間にモデルを当てはめること
最も基本的なモデルは y = ax + b という形式の線形回帰である
Wikipedia
Wikipediaの定義の説明は、難しい単語が並んでしまっています…
目的変数（y）と説明変数（x）の間にモデルを当てはめるとありますが、言葉を少し変えてみましょう
・目的変数とはあなたが「知りたい」情報のことで、分析結果の数値とします
・説明変数とは「影響を与える」データのことで、分析結果の要因となる数値です
つまり回帰分析とは…
結果に影響を与える情報を使って、知りたい値を導き出す分析
よく例に出てくる「身長」と「体重」を使って上記の定義に当てはめてみます
あなたが知りたいのは「体重」で、それに影響を与えるのが「身長」とします
（結果に影響を与える）身長を使って、（知りたい値）体重を導き出す分析
これは非常にイメージが湧きやすいのではないでしょうか？
今回は人間の「身長」と「体重」のデータではなく、ポケモンの「高さ」と「重さ」のデータを使います
ポケモンのデータとは？
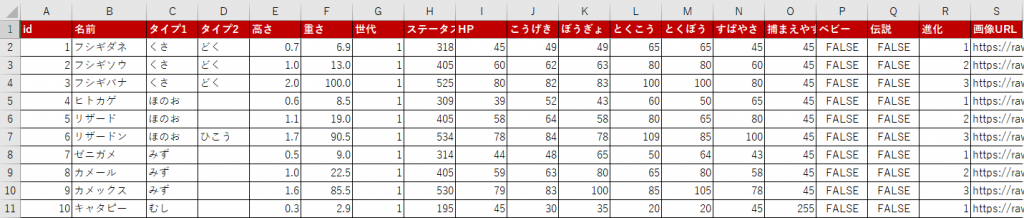
今回利用しているポケモンのデータはPoke APIを利用することで、無料でデータを取得することができます
Excelデータもご用意しているので、ぜひ手元で確認してみてください
ポケモンで学ぶデータ分析｜データの中身を知ろう
単回帰・重回帰の違いは？
単回帰分析と重回帰分析の違いはずばり「説明変数の数」です
結果に影響を与える情報である「説明変数が1つ」の場合は「単回帰分析」で、「説明変数が2つ以上」の場合は「重回帰分析」を実施することになります
2つには計算式が存在しており、非常に簡単な式で表すことができます
単回帰：y = ax + b
重回帰：y = a1x1 + a2x2 + a3x3 … + b
目的変数（y）を求めるために、説明変数（x）に加えて係数（a）と 切片（b）を組み合わせた式になり
重回帰の場合は説明変数（x）と係数（a）が複数になります
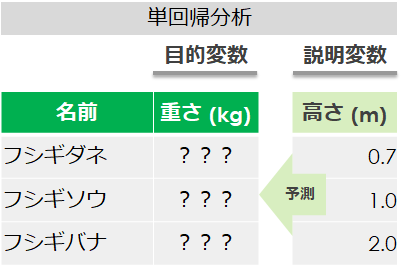
単回帰分析を実施する
まずは「単回帰分析」をからご説明していきます
単回帰分析とは「1つ」の説明変数（結果に影響を与える値）から、目的変数（知りたい値）を算出する方法です
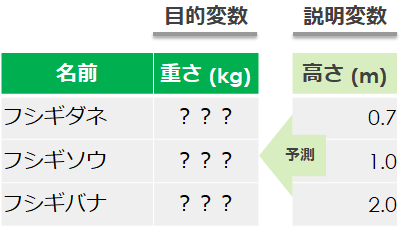
今回は例のように「高さ」だけのデータを用いて、「重さ」を予測してみます
また単回帰分析の式はこちらです
y = ax + b
単回帰の式を求める方法は、散布図を描くだけで簡単に算出することができます
それではポケモンの「高さ」を横軸、「重さ」を縦軸に並べた散布図を作成します
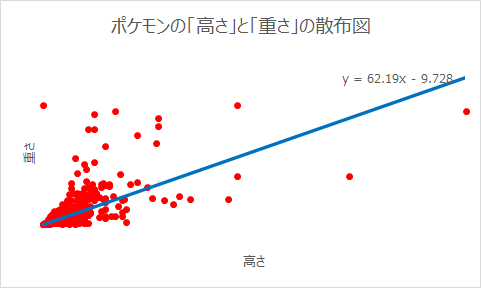
式を入れると下記のような式が出てきました
y = 62.19x – 9.728
yは目的変数を、xは説明変数を示しているので、分かりやすいように置き換えます
重さ = 62.19（ｘ高さ） – 9.728
さらに分かりやすいように言い換えると下記になります
ポケモンの重さは…高さに62.19を掛けて、9.728を引くと計算できる
実際のデータで検証してみる
それでは上の式から計算した「単回帰分析の結果」と「実際の重さ」を比較してみます
No.1-3のポケモンで検証してみます
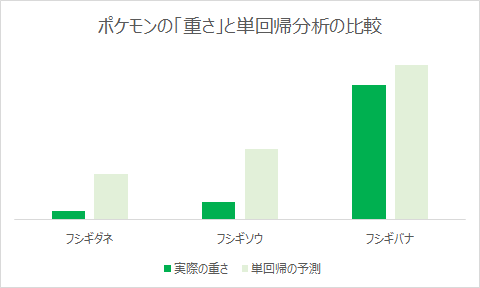
ポケモンの「高さ」だけを使って「重さ」を予測したところ、最終進化のフシギバナだけ実際の値と近い結果となりました
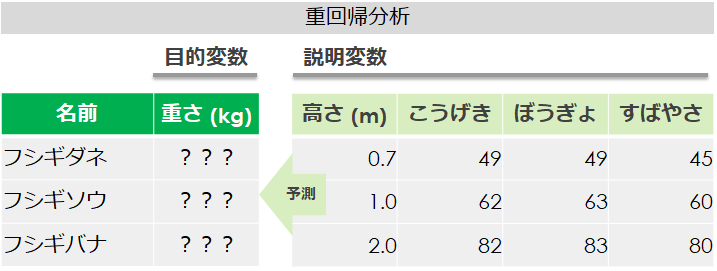
重回帰分析を実施する
続いて「重回帰分析」を実施します
単回帰分析は「1つ」の説明変数を利用したのに対し、
重回帰分析は「2つ以上」の複数の説明変数を利用して、目的変数を予測していきます
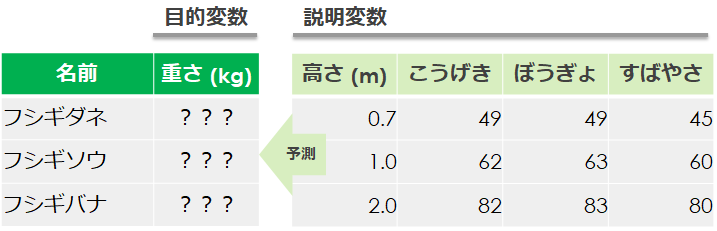
予測するための材料（説明変数）が多いため、重回帰分析の方が精度が良くなる傾向があります
今回は目的変数である「重さ」を、4つの説明変数「高さ・こうげき・ぼうぎょ・すばやさ」を使い予測します
先ほどと同様に式に当てはめて計算していきます
y = a1x1 + a2x2 + a3x3 … + b
重回帰分析を実施するにはExcelやPythonなどを利用することで、瞬時に算出することができます
Excelで分析した結果を見てみましょう
エクセルで回帰分析を実施する方法はこちらからご覧ください
【エクセル】回帰分析を簡単に実施する方法を解説します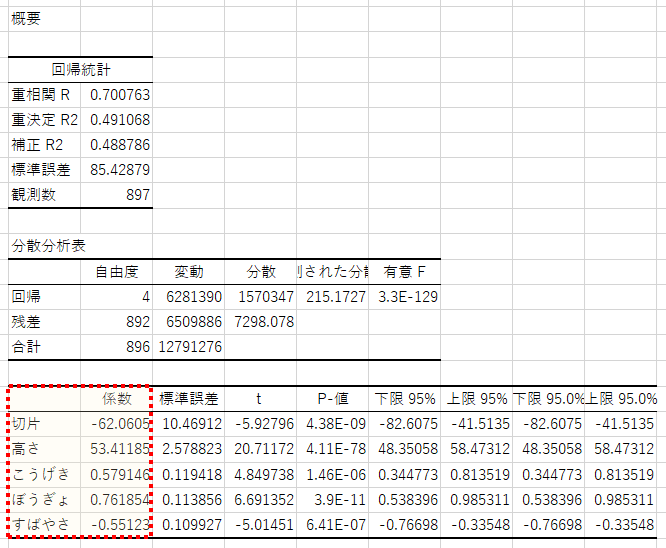
いろいろな統計結果が出てきますが、係数の部分に注目しましょう
重さ = 53.41 ×（高さ）
+ 0.579 ×（こうげき）
+ 0.761 ×（ぼうぎょ）
– 0.551 ×（すばやさ）
– 62.06
このような数式が完成しました
少々複雑ではありますが4つの説明変数「高さ・こうげき・ぼうぎょ・すばやさ」を使って、ポケモンの重さを予測することができます
実際のデータで検証してみる
こちらも「実際の重さ」と「重回帰分析」の結果を比較してみます
また事前に用意した「単回帰分析」とも比較してみましょう
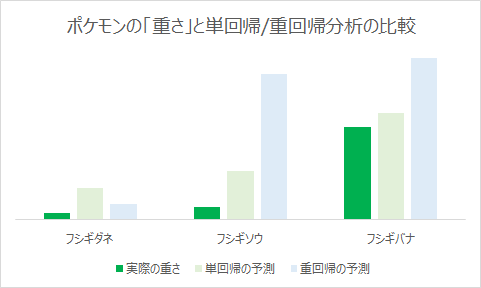
左の「フシギダネ」は単回帰分析よりも高精度で予測ができています
一方で「フシギソウ」「フシギバナ」の2匹のポケモンに関しては、単回帰分析の方が実際の結果に近い結果でした
まとめ
今回はポケモンのデータを用いて「回帰分析」をご紹介してきました
回帰分析を利用することで、店舗の売上のデータや仕入れの予測などを実施することができます
データ分析の基礎となる手法なのでぜひ使いこなしてみてください
相関関係とは？分かりやすく解説｜ポケモンで学ぶデータ分析
