Smart-Hint 
目次
評価指標のAUCとは？
AUC（Area Under the Curve）は機械学習の「分類」タスクにおける、正である場合の確率を予測する場合に利用する評価指標です
ROC曲線（Receiver Operating Characteristic Curve）が描く曲線をもとにAUCは計算されます
AUCは「面積」のことで、ROC曲線は「線」を示しています
いきなり聞きなれない英字が出てきましたが、それぞれ分かりやすく解説していきます
まず分類における確率の予測とは？
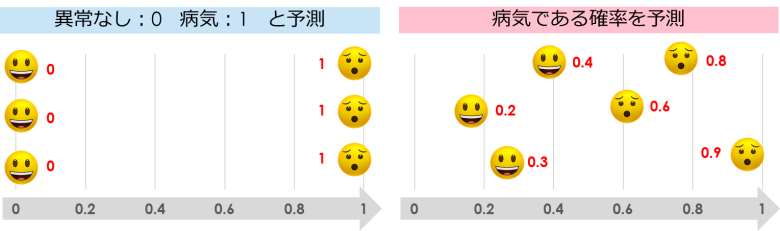
分類を予測する場合、最終的なアウトプットは2つパターンがあります
- 「0」か「1」を予測（病気であれば「1」異常なしであれば「0」）
- 正である場合の確率を予測（病気である確率が「0.85」）
1つ目の「0 / 1」の二値分類の評価指標については、混同行列（Confusion Matrix）を用いた評価指標を利用します
こちらで解説しているのでぜひご覧ください
【機械学習】分類の評価指標を一番分かりやすく解説｜confusion-matrix
今回は2つ目の正である場合の確率を予測する方法としてAUCを解説します
AUCの定義
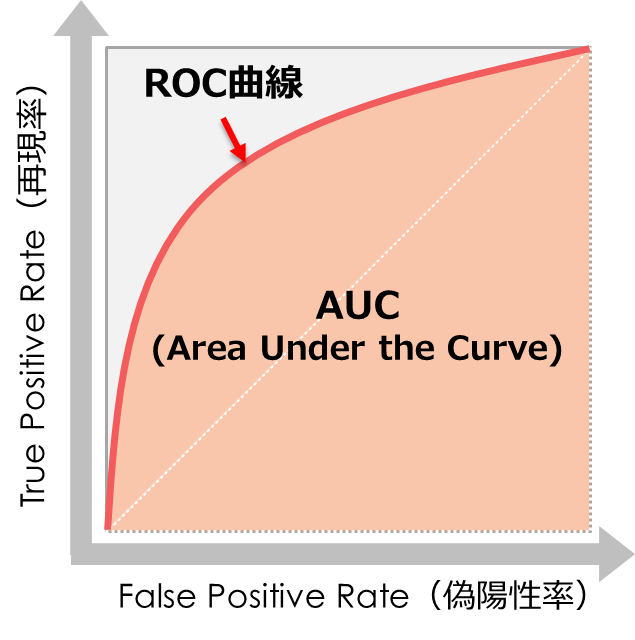
AUCはROC曲線が描く曲線が示す「面積」のことです
そしてROC曲線は、予測値を正とする閾値を「0」から「1」へ動かしたときの「偽陽性率」と「再現率」をプロットすることで描くことができます…（詳しくは後述します）
つまり「偽陽性率」と「再現率」を掛け合わせたものがAUC（面積）となります
- 「偽陽性率」と「再現率」ともに最大値が1になる確率であるため、AUCの面積も最大値は「1 x 1 = 1」となる
- 「偽陽性率」と「再現率」は背反する指標のため、AUCの最小値は「0.5」となる（0ではない）
AUCで理解しにくいのは、「閾値を1から0へ動かしたとき」の部分かと思います
イメージをしっかり持っていただくために、グラフィックを用いて流れを解説します
ROC曲線を描く流れ
今回「病気を予測する機械学習」を事例として利用します
病気である確率を「1」として、その確率を予測していきます
① もし完璧な予測モデルがあれば…
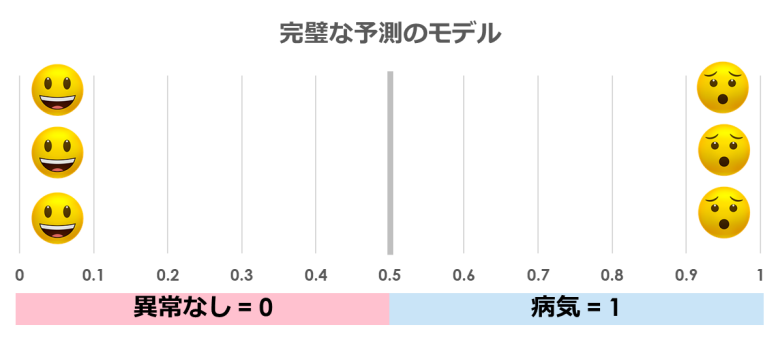
確率を予測するモデルですが、もし完璧なモデルを作ることができれば「0：異常なし」か「1：病気」の二値だけの結果になります
② 確率を予測するモデルの実態
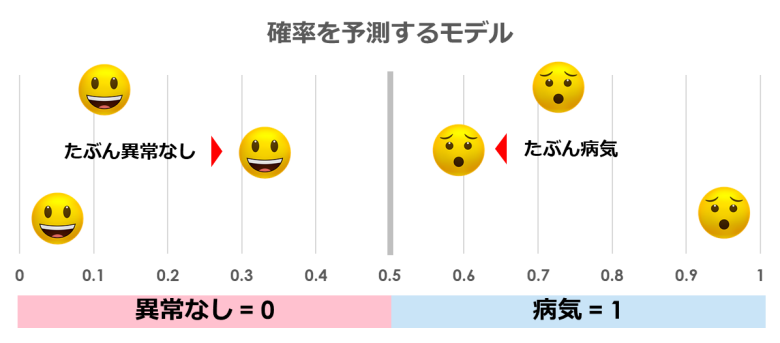
もちろん完璧なモデルは作成できないので、確率がバラバラなモデルになります
つまり「0.3」のたぶん異常がない人がいたり、「0.6」のたぶん病気な人がいたりします
③ ただし間違える場合もある
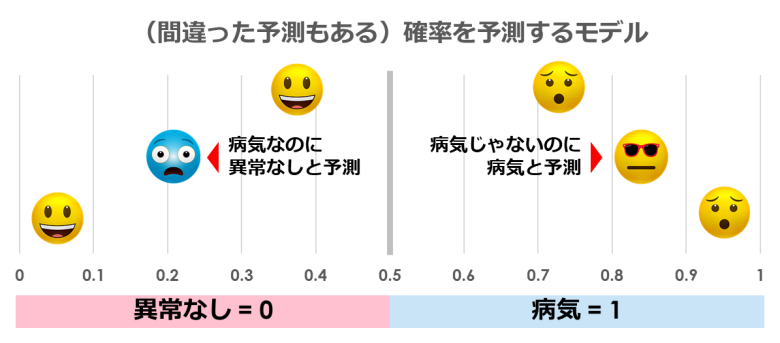
確率を予測するとき、当然間違って予測してしまうことがあります
例えば実際は病気なのに「異常なし」と診断したり、逆に病気ではないのに「病気」と診断したりする場合があります
④ 閾値を「0.5」にして2つのグラフにしてみる
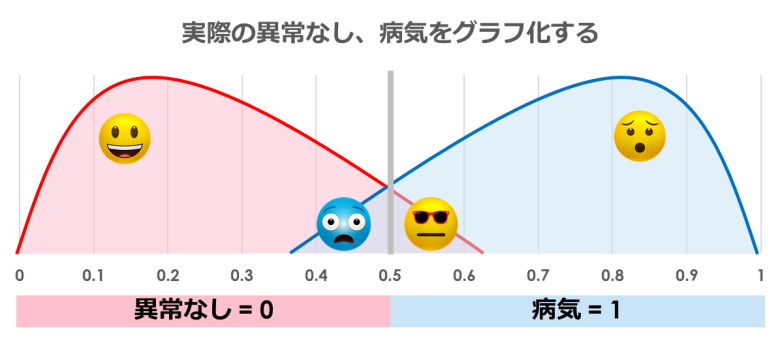
実際の「異常なし」と「病気」を2つのグラフにしてプロットしてみます
閾値を「0.5」に設定すると、前述のとおり間違って予測してしまう場合が出てきます
※グラフのクロスしたところが、間違って予測してしまっている部分です
⑤ 偽陽性率を算出する
偽陽性率（False Positive Rate）は、実際に異常なし（Negative）の中で予測が間違っていた割合です
山の右側の「病気ではないが誤って病気と診断してしまった」割合となります
⑥ 再現率を算出する
再現率（True Positive Rate）は、実際に病気（Positive）の中で、予測が合っていた割合です
山の右側の「実際に病気で、正しく診断できた」割合になります
⑦ 偽陽性率と再現率をプロットする
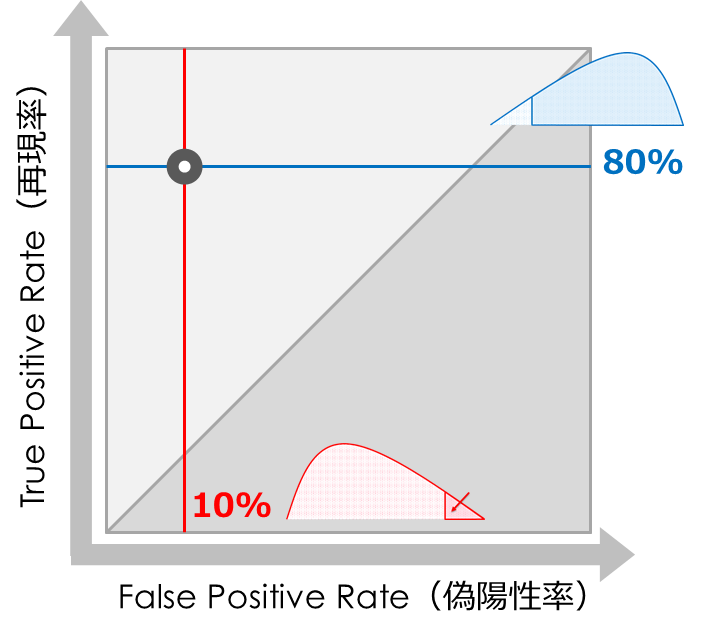
算出した「偽陽性率」と「再現率」の2つをX軸・Y軸に取りグラフを作ります
上記の事例では「偽陽性率＝10%」と「再現率＝80%」をプロットします
⑧ 閾値を変えてみて、再度プロットする
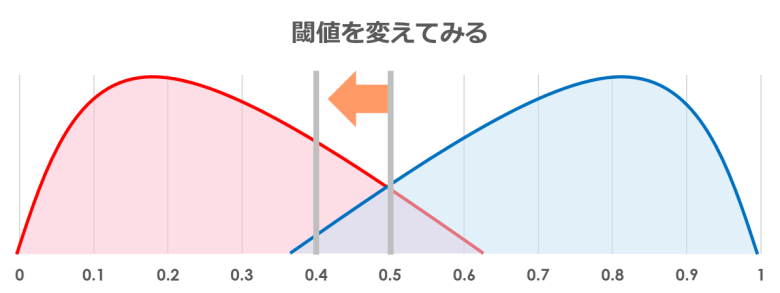
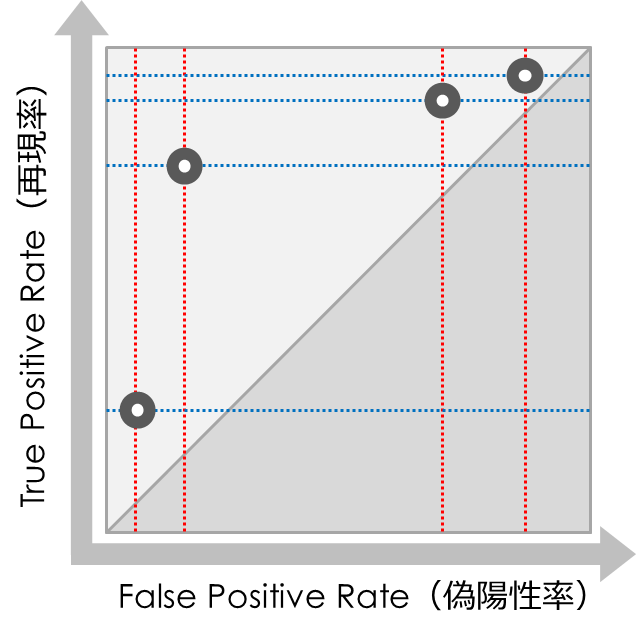
先ほど「0.5」に設定した閾値を変えて、先ほどのプロットを続けます
「偽陽性率」と「再現率」は正方形の左上部分のみプロットされます
片方が上がると、もう片方も上がる関係になっています
⑨ 閾値を0から1にしてつなげる
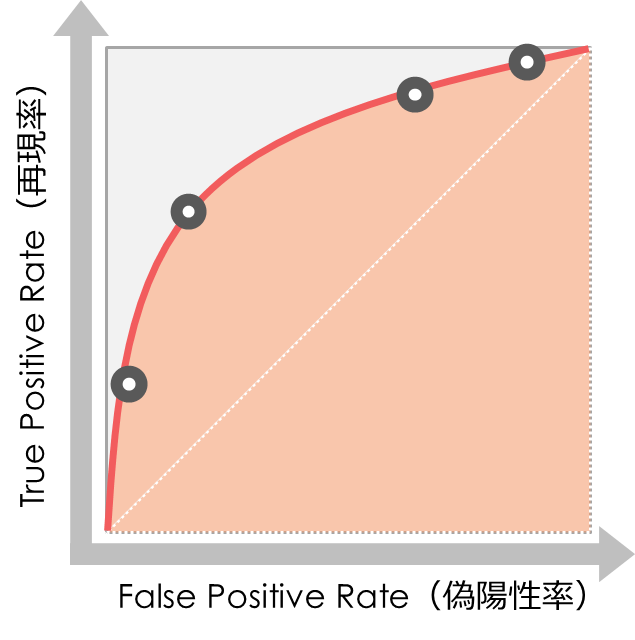
最後に閾値を「0」から「1」のすべてを試し、線としてつなげます（ROC曲線）
正方形「1 x 1」を全体として、曲線までの面積がAUCとなります
AUCの解釈の仕方
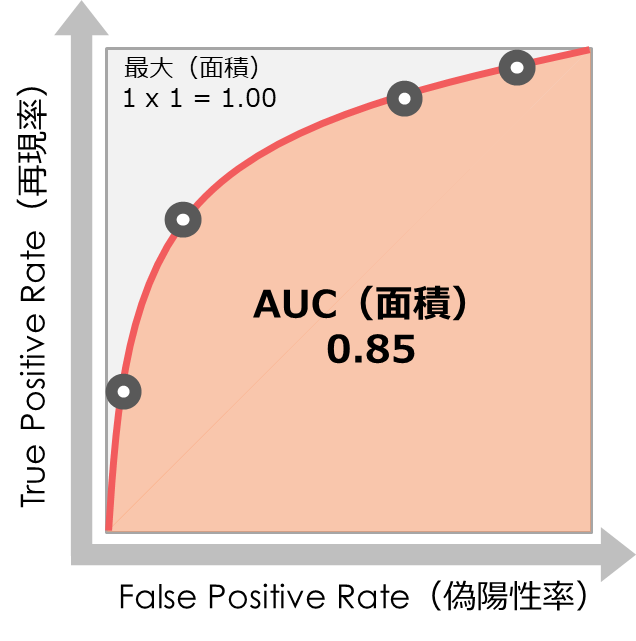
AUCは数値が大きければ大きいほど精度が高くなる指標です
つまり最大値である「1」に近ければ精度が高く、最小値「0.5」に近ければ精度が低いことになります
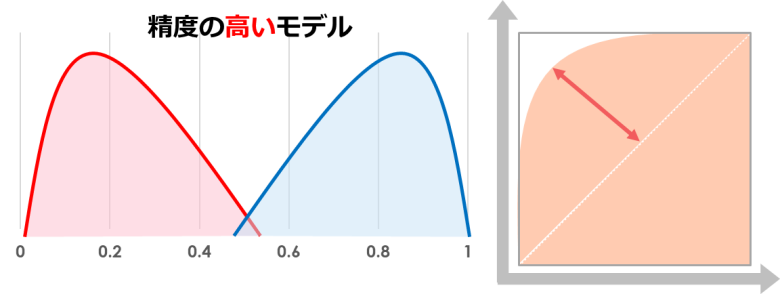
精度の高いモデルは閾値で交差する部分が少なく、誤った予測が少ないため面積は大きくなります
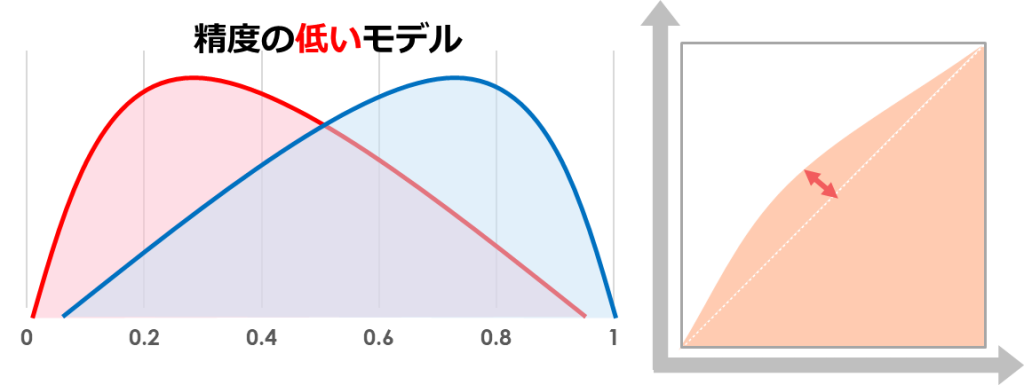
一方で精度の低いモデルは、誤った予測が多くなるためAUCの面積は小さくなります
AUCの算出方法
最後にPythonを利用して、AUCを簡単に算出する方法をご紹介します
実際の値（y_test）と予測値（y_pred）を用意します
y_test = [1,1,1,0,0,0]
y_pred = [0.9, 0.6, 0.2, 0.1, 0.2, 0.7]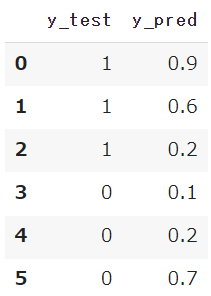
sklearn.metricsからroc_auc_scoreをインポートします
from sklearn.metrics import roc_auc_score
roc_auc_score(y_test, y_pred)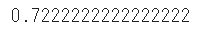
実際の値と予測した値の2つのリストを代入することで、AUCを簡単に算出することができました
まとめ
今回は機械学習「分類」タスクにおける、正である場合の確率を予測する場合に利用する指標であるAUCについてご紹介してきました
またグラフィックを用いてROC曲線の書き方もご紹介しています
最終的なアウトプットの理解はもちろんですが、どうしてそのグラフになるのかを理解することは重要です
他の指標についても解説しているのでぜひご覧ください
【機械学習】分類の評価指標を一番分かりやすく解説｜confusion-matrix
