Smart-Hint 
目次
主成分分析（PCA）とは？
主成分分析（PCA：Principal Component Analysis）とは次元削除の代表的な手法です
多次元データのもつ情報をできるだけ損わずに、低次元空間に情報を縮約することができます
多次元とはつまり「たくさんの情報」という意味で、
次元削除とは「より少ない情報に要約」することを指します
例えば多次元のデータとして「国語」「数学」「英語」の3教科のテストの点数があります
要約として「総合点」を割り出します
これが一番シンプルな次元削除のイメージです
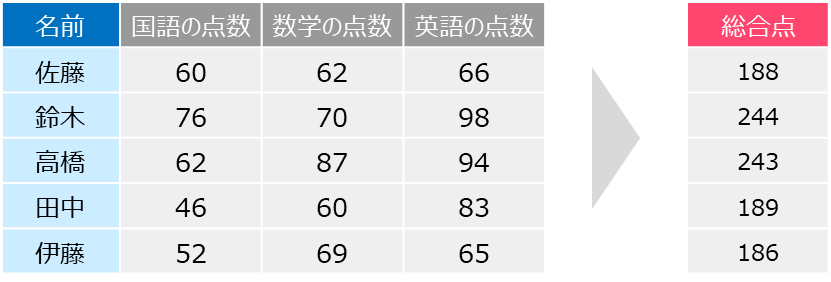
しかし単純に合計点を出せばよいわけではありません
下記のような13列あるデータに対して、主成分分析（PCA）を実施するとこでより少ない情報（列）に要約することができます
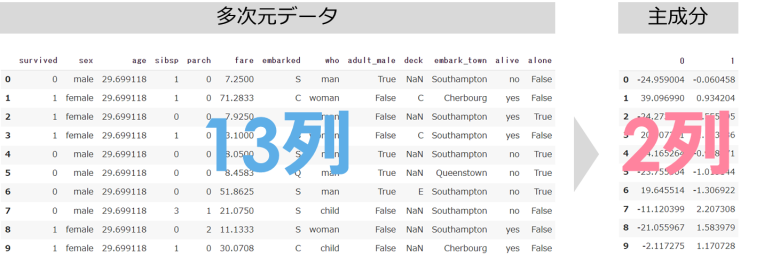
主成分分析（PCA）では最終的な主成分がより多くの情報を持つために、データの分散に着目します
そしてこの分析を実施する目的は2つです
- 情報量の多いデータを要約することで特徴を可視化する
- 新しい変数として機械学習モデルの精度を向上させる
主成分分析の事前準備
Seabornから、タイタニック号のデータを取得しておきます
またPandasも合わせてインポートしておきます
import seaborn as sns
import pandas as pd
df = sns.load_dataset('titanic')
df.head()
【Python】初心者向けタイタニック号のサンプルデータをご紹介します
ラベルを定義しておく ※任意
主成分分析（PCA）の処理に必須ではありませんが、次元削除した後に正しさを可視化するために
ラベルとしてclass（チケットクラス）を定義します
label = df['class']
欠損値を処理する
まずはisnullとsumを組み合わせて、欠損値を確認します
df.isnull().sum()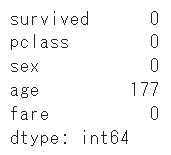
「年齢」に177件の欠損が確認できたので、今回は平均で補いましょう
fillnaを使います
mean = df['age'].mean()
df['age'] = df['age'].fillna(mean)
【Python】欠損値の扱い方大全
ダミー変数処理（文字列→数値）
主成分分析（PCA）では、数値型しか扱えないためダミー変数処理を行います
df = pd.get_dummies(df, drop_first=True)
【Python】カテゴリ変数の数値変換｜ダミー処理（one-hot encoding / label encoding）
主成分分析（PCA）のPython実装
前処理が完了したのでsklearnからPCAをインポートして主成分分析を行います
n_componentsで取得する主成分の数（列数）を指定することができます
※今回は情報を一番多く含む「第一主成分」と、次に多く含む「第二主成分」を抽出します
from sklearn.decomposition import PCA
pca = PCA(n_components=2)定義した変数（df）に対してfit_transformを利用し変換を行います
結果がarray形式で出力されるため、DataFrameに変形する処理を行っています
df_pca = pd.DataFrame(pca.fit_transform(df))
df_pca.head()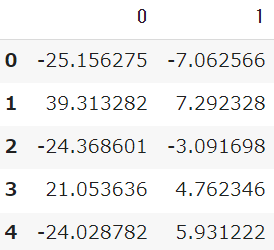
主成分分析（PCA）の可視化
主成分分析（PCA）の結果だけでは人間が理解しにくいため、散布図を使って可視化します
単純に可視化するだけではデータのばらつきしか見えないため、事前に準備したラベル（チケットクラス）で分割します
df_pca['label'] = label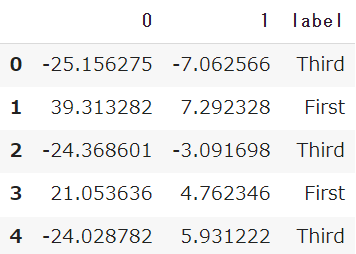
Seabornを使って可視化します
sns.scatterplot(data=df_pca, x=0, y=1, hue='label')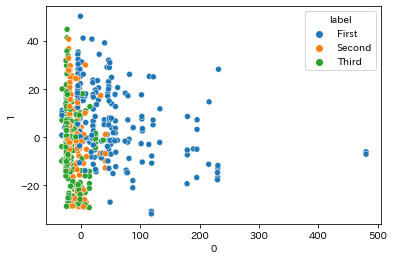
第一主成分（横軸）では、チケットクラスの分類がうまくできています
第二主成分（縦軸）では3つのラベルが混じっているため、他に分割できる情報があるかもしれません
寄与率
第何主成分がどのくらいの情報を説明できるかを「寄与率」で確認することができます
※基本的には第一主成分が最も情報量（ばらつき）のある軸になります
explained_variance_ratio_を使うことで寄与率を算出することができます
pd.DataFrame(pca.explained_variance_ratio_)
この結果から第一主成分で「93%」の情報が含まれることが分かりました
第二主成分も含めると「99%」の寄与率になります
つまり多次元の情報をたった2つの軸だけで、ほとんどの情報を可視化することができました
まとめ
今回はPythonを利用して次元削除の最もポピュラーな手法である「主成分分析（PCA）」をご紹介してきました
非常に簡単に多次元のデータを要約することができます
機械学習モデルの精度向上に利用してみてください
# 事前準備
import seaborn as sns
import pandas as pd
from sklearn.decomposition import PCA
# タイタニック号のデータを取得
df = sns.load_dataset('titanic')
# チケットクラスのラベルの取得
label = df['class']
# 欠損値の確認と変換
df.isnull().sum()
mean = df['age'].mean()
df['age'] = df['age'].fillna(mean)
# ダミー変数化
df = pd.get_dummies(df, drop_first=True)
# 主成分分析（PCA）の実装と変換
pca = PCA(n_components=2)
pca.fit(df)
df_pca = pd.DataFrame(pca.transform(df))
# 主成分分析（PCA）変換したデータにラベルを付与する
df_pca['label'] = label
# Seabornで散布図を可視化する
sns.scatterplot(data=df_pca, x=0, y=1, hue='label')
# 主成分分析（PCA）の寄与率を算出する
pd.DataFrame(pca.explained_variance_ratio_)
