目次
線形回帰とは?
今回はPythonを使って線形回帰(LinearRegression)の機械学習のモデルを作成する方法をご紹介します
「回帰」とは、結果に影響を与える情報(説明変数)を使って、知りたい値(目的変数)を導き出す機械学習の分析です
その中でもシンプルなモデル式である線形回帰は、ビジネスシーンでもよく用いられる手法です線形回帰の詳細な説明は下記サイトにて解説しているのでご覧ください
 回帰分析とは?分かりやすく解説|ポケモンで学ぶデータ分析
回帰分析とは?分かりやすく解説|ポケモンで学ぶデータ分析 事前準備
Seabornから、チップ価格のサンプルデータを取得しておきます
またPandasも合わせてインポートしておきます
import seaborn as sns
import pandas as pd
df = sns.load_dataset('tips')
df.head()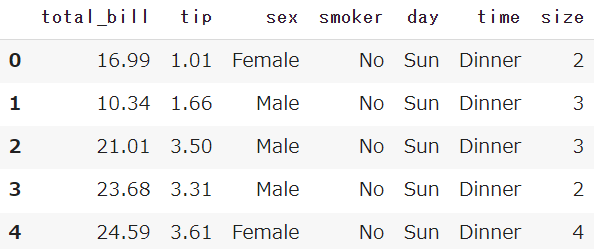
 【Python】チップ価格のサンプルデータをご紹介
【Python】チップ価格のサンプルデータをご紹介 線形回帰の前処理
欠損値の処理
まずは事前に定義した変数(df)に、欠損値(null)が無いか確認しましょう
※線形回帰は欠損値を処理することができません
df.isnull().sum()
今回は欠損値が無いことが分かりました
欠損値が存在していた場合は、fillnaやdropnaで処理してください
 【Python】欠損値の扱い方大全
【Python】欠損値の扱い方大全説明変数(x)と目的変数(y)に分割
チップの額を予測するため、説明変数(x)からtipを取り除き、目的変数(y)をtipだけに絞ります
df_x = df.drop('tip', axis=1)
df_y = df['tip']ダミー変数処理(文字列→数値)
get_dummiesで文字列型のデータを数値型(0-1)に変換します
df_x = pd.get_dummies(df_x)
 【Python】カテゴリ変数の数値変換|ダミー処理(one-hot encoding / label encoding)
【Python】カテゴリ変数の数値変換|ダミー処理(one-hot encoding / label encoding)学習用-テスト用に分割
train_test_splitを使って、学習用とテスト用にデータを分割します
from sklearn.model_selection import train_test_split
train_x, test_x, train_y, test_y = train_test_split(df_x,df_y,random_state=5)
 【機械学習】学習-テストデータに分割(hold-out法)|train_test_split
【機械学習】学習-テストデータに分割(hold-out法)|train_test_split線形回帰モデルの作成と予測
まずは線形回帰(LinearRegression)のモデルを作成します
from sklearn.linear_model import LinearRegression
model = LinearRegression()上記で前処理を実施したデータをfitメソッドで学習を行います
model.fit(train_x,train_y)モデルに対してpredictで予測を実施します
pred = model.predict(test_x)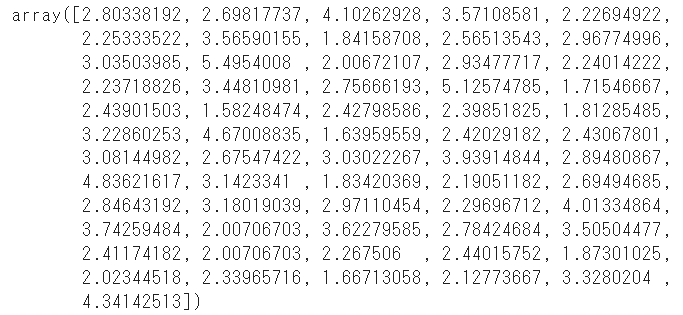
線形回帰の係数と切片の算出
線形回帰は学習済みのモデルから計算式を算出することができます
目的変数(y)を予測するために、説明変数(x)に加えて係数と切片を利用します
y(目的変数) = a(係数) * x(説明変数) + b(切片)
係数の算出はcoef_を利用します
係数は説明変数(x)の順番に出力されます
print(model.coef_)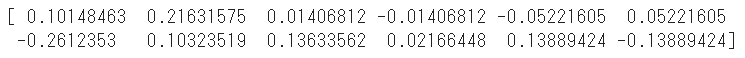
切片の算出はintercept_を利用します
print(model.intercept_)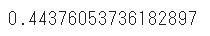
係数をDataFrameで表示する
説明変数の順に算出されるcoef_と、説明変数の「列名」を組み合わせて、DataFrameを作成します
説明変数(x)が1上がるごとに、どのくらい目的変数(y)に変化があるかを可視化することができます
df_coef = pd.DataFrame(model.coef_)
df_coef.index = train_x.columns
df_coef.style.bar()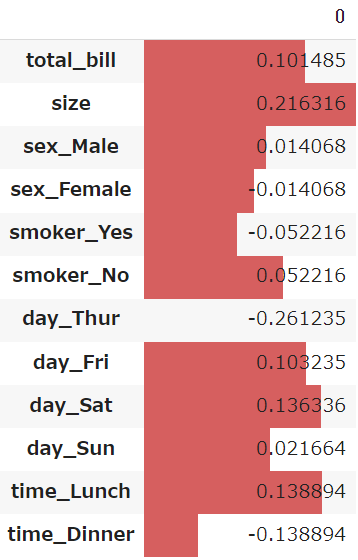
線形回帰の評価
上記で作成した機械学習のモデルと予測値(pred)が、どのくらい正確なのかを評価していきます
結果となる値(test_y)が存在しているので、この2つを比較します
比較方法はRMSE(平均平方二乗誤差)と呼ばれている方法を利用します
RMSEは最小値=0で、小さければ小さいほど良い指標です
 【機械学習】回帰の評価指標RMSE(平均平方二乗誤差)を分かりやすく解説
【機械学習】回帰の評価指標RMSE(平均平方二乗誤差)を分かりやすく解説RMSEの算出
sklearnからmean_squared_errorをインポートし、numpyで平方根を付けます
from sklearn.metrics import mean_squared_error
import numpy as np
rmse = np.sqrt(mean_squared_error(test_y,pred))
rmse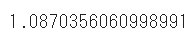
一般的な感覚との比較
今回の機械学習で利用したチップ価格は、一般的には総額の「15~20%」と言われています
total_bill(総額)だけの情報でチップ額を予測し、RMSEで評価してみます
tip_20 = test_x['total_bill']*0.20
rmse = np.sqrt(mean_squared_error(test_y,tip_20))
rmse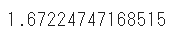
機械学習のモデルと比較して、RMSEが高くなっています
RMSEは小さいほど精度が高いモデルを示すため、機械学習の予測の方が優れていることが分かります
チップ額の予測を「1%」から「40%」までそれぞれ実行して、機械学習の予測と比較します
result = []
num = []
result_df = pd.DataFrame()
for i in range(1,40):
tip_num = test_x['total_bill']*(i/100)
rmse = np.sqrt(mean_squared_error(test_y,tip_num))
result.append(rmse)
num.append(i/100)
pd.DataFrame(result,num).plot.bar(figsize=(12,4), legend=False)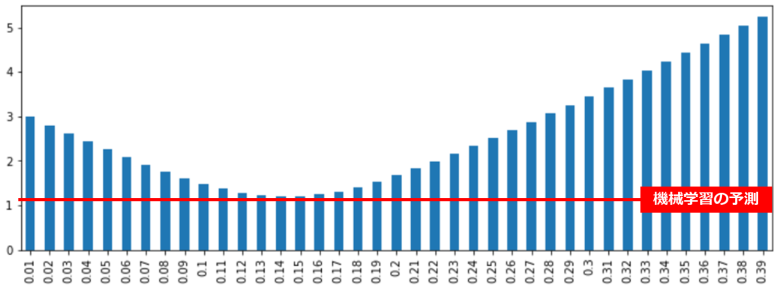
「14%」あたりが最もRMSEが低くなりますが、それでも機械学習の予測には届きませんでした
まとめ
今回はLinearRegressionをPythonで実施する方法についてご紹介しました
回帰分析は簡単に予測を行えることに加えて、どの要素が影響を与えているかを可視化することができます
ぜひ活用してみてください
全てのコード
# 事前準備
import seaborn as sns
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
import numpy as np
# チップ価格のサンプルデータを取得
df = sns.load_dataset('tips')
# 説明変数と目的変数に分割
df_x = df.drop('tip', axis=1)
df_y = df['tip']
# 前処理(ダミー変数化と欠損処理)
df_x = pd.get_dummies(df_x)
df_x.head()
# 学習用-テスト用に分割
train_x, test_x, train_y, test_y = train_test_split(df_x,df_y,random_state=5)
# 線形回帰のモデル作成と予測
model = LinearRegression()
model.fit(train_x,train_y)
pred = model.predict(test_x)
# モデルの評価
rmse = np.sqrt(mean_squared_error(test_y,pred))
print('モデルの評価[RMSE]',rmse)
# 係数と切片の算出
df_coef = pd.DataFrame(model.coef_)
df_coef.index = train_x.columns
df_coef.style.bar()
 Smart-Hint
Smart-Hint